This is the moment we've been working up towards. We're finally going to build an AI to try to play Block Sudoku. So disclaimer, I'm not an expert in this, so my resulting network will most likely be far from optimal. It honestly took me a week or two of trial and error and debugging just to get the model to stabilize and actually start to converge.
Reinforcement Learning
We're going to use Reinforcement learning as a basis for developing our AI Block Sudoku agent. In Reinforcement learning, our agent attempts to learn the solution to a problem through trial and error without any input from a human. Our goal is to develop an agent that will attempt to choose the action that best maximizes it's score. Our agent is given an environment and chooses an action from a given policy to take. Then it's given the new state of the environment (observation) along with the reward for that action.
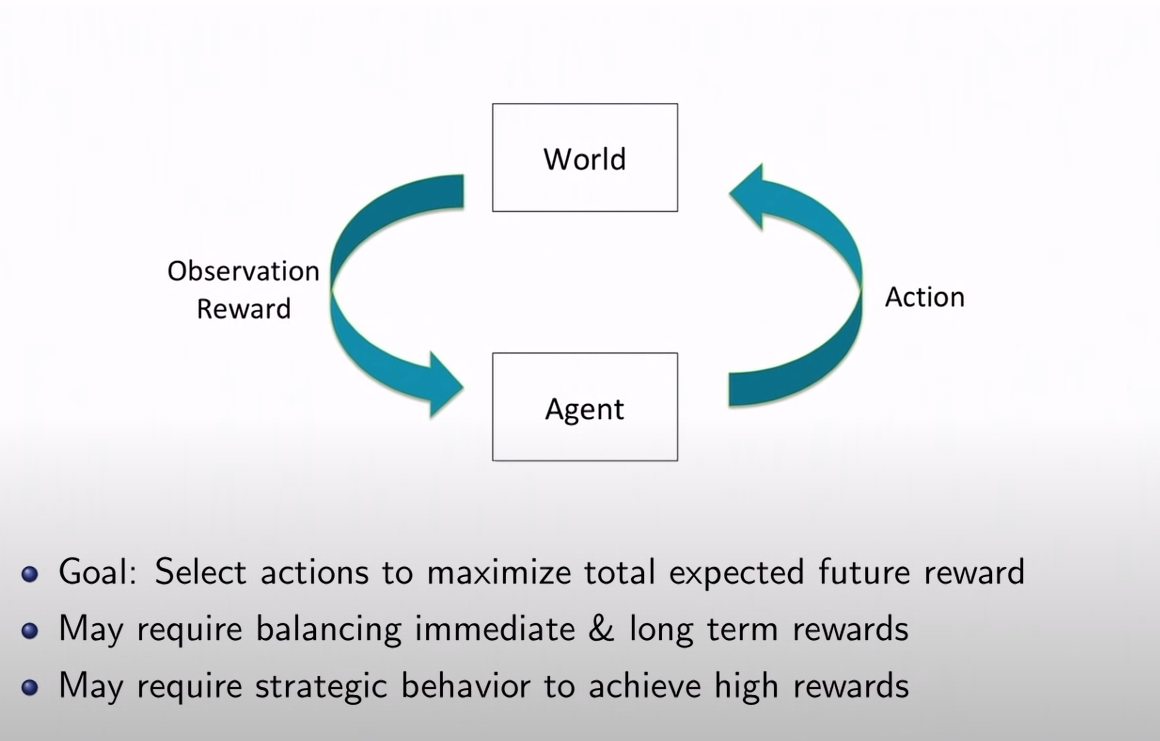
Our observation and action space will reflect the same observation and action space we've set up in the last post. For our reward function, every time the agent makes an invalid move, it receives -1 reward. A correct move generates 0 reward. Clearing lines will result in a reward equal to the score earned so clearing multiple lines at once is encouraged.
Deep Q-Learning
The particular technique we're going to use is the tried and true Deep Q-Learning, which uses a Neural Network to approximate Q-values versus traditional Q-learning which would involve keeping a large Q-table in memory. Like a lot of other projects you may see using Deep Q-Learning for games, the techniques and network structure I'm using for my network are heavily based on the famous 2013 Deep Mind paper [2].
If you're not familiar with Q-learning or need a quick recap, a very brief introduction to Q-Learning and general algorithm for it can be found here. Another important addition not explained in that introduction is the use of a target and source network to estimate the Q-values. After a set amount of frames, the weights of the target network are updated. I also am implementing experience replay, which involves sampling a batch of past experiences to train the network. You can find expanded explanations of these techniques here under "Solutions".
Building the First Model
I built the first few models in the spirit of DeepMind... and the performance was less than stellar. I first dealt with loss explosion after 1000 episodes, which in my previous experiences, usually attributed to gradient vanishing/explosion. However having already implemented gradient clipping and my lowering the learning rate, the problem still wasn't solved. Interestingly, it turned out to how python was handling the numbers. The observation space was being passed as a matrix of integers, and for some reason python was having trouble with the calculations on it. Simply casting the observation space to floating point fixed my whole issue with loss explosion. Odd!
I switched the network to Adam as Adam will usually converge faster, and used standard MSE for the loss function.
optimizer = keras.optimizers.Adam(learning_rate=0.01)
loss_function = keras.losses.MeanSquaredError(reduction="auto", name="mean_squared_error")
The model was overfitting a bit, so I had to lower the number of parameters to achieve a better result. Since our reward can be anywhere from -10 to 10, the output layer was changed to linear versus the usual SoftMax layer.
def create_q_model():
# Network defined by the Deepmind paper
inputs = layers.Input(shape=(15, 15, 1))
layer1 = layers.Conv2D(16, 3, strides=3, activation="relu")(inputs)
layer2 = layers.Conv2D(32, 3, strides=1, activation="relu")(layer1)
layer4 = layers.Flatten()(layer2)
layer5 = layers.Dense(64, activation="relu")(layer4)
action = layers.Dense(num_actions, activation="linear")(layer5)
return keras.Model(inputs=inputs, outputs=action)
return model
There are a few other hyperparameters that I've modified, most notably reducing the amount of exploration. Since the blocks in the queue are already randomized, the state transitions will almost always be different so exploration already happens naturally just by playing the game. This may pose an issue later, (ex. what is the optimal move when we only have one block in queue when we don't know what the new queue will look like?). Epsilon in our epsilon-greedy policy will decrease to 1% instead of 10%, but honestly we can probably get away with having it at 0%. Having a small gamma of 0.2 (discount factor) causes the network to favor more immediate rewards since at most, we can only plan 2 moves ahead anyways.
gamma = 0.2 # Discount factor for past rewards
epsilon = 1.0 # Epsilon greedy parameter
epsilon_min = 0.01 # Minimum epsilon greedy parameter
epsilon_max = 1.0 # Maximum epsilon greedy parameter
epsilon_interval = (
epsilon_max - epsilon_min
)
epsilon_greedy_frames = 10000.0
# ```We'll also update the target network at shorter intervals.
update_after_actions = 30
update_target_network = 100
To avoid the network picking the same invalid action over and over and staying in the same state, I restricted the network to only executing valid actions. Our potential action space will at most be 9*9*3 = 243, as we can have 3 blocks in queue and 9x9 potential places to put them on the board. This is a much larger action space than DeepMind or Atari games, and it was difficult to find literature where anyone used an action space as large as this. It may come back to bite me in the butt later, or cause the network to converge slower. Since we choose the action to generate the max potential reward, we can simply mask invalid actions with -Inf to make sure they never get chosen when we find the optimal action with argmax().
# Grab action Q-values from the model
state_tensor = tf.convert_to_tensor(state, dtype=tf.float32)
state_tensor = tf.expand_dims(state_tensor, 0)
action_probs = model(state_tensor, training=False)
# Mask invalid moves with -inf
valid_moves = env.get_valid_action_space()
valid_moves[valid_moves == 0] = -inf
valid_action_probs = np.multiply(valid_moves, action_probs[0])
valid_action_probs[valid_action_probs == inf] = -inf
# Take (valid) best action
action = tf.argmax(valid_action_probs).numpy()
Before I run the model, it should be noted that for puzzle and board games, Monte-Carlo Tree Search is used more often in conjunction with Reinforcement Learning [3], but I haven't implemented that in my network. It may be something I need to revisit later.
Running the model
After training and a few days of playing around with the hyperparameters, the performance was... less than satisfactory. Here's the best model I was able to produce compared to randomly selecting moves. This was trained over 250,000 iterations of the game.
| Game | Random | RL | Human |
|---|---|---|---|
| 0 | 1 | 3 | 11 |
| 1 | 0 | 10 | 5 |
| 2 | 4 | 0 | 17 |
| 3 | 1 | 4 | 19 |
| 4 | 0 | 0 | 31 |
| 5 | 1 | 0 | |
| 6 | 1 | 2 | |
| 7 | 4 | 0 | |
| 8 | 1 | 11 | |
| 9 | 1 | 0 | |
| Avg | 1.4 | 3.0 | 17.0 |
It only performs twice as good as random, but is far, far from human-level performance. The model stagnated after around 150,000 iterations and didn't really make any progress from iteration 150k to 250k. I've already spent a good amount of time working out the network, figuring out what it should be learning, and reading papers to try to understand how to build an optimal network for this problem. At this point, I may need to take a break and try a new approach.
References
[1] https://www.youtube.com/watch?v=FgzM3zpZ55o&feature=emb_title
[2] https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
[3] https://www.researchgate.net/publication/220978338_Monte-Carlo_Tree_Search_A_New_Framework_for_Game_AI (May be behind paywall for public)

