I've been addicted to No Man's Sky, especially with all the frequent and awesome content the developers over at Hello Games have been putting out for it. Despite it's horrible initial launch, I commend the devs for sticking to it out and making it a blast to play. In the words of one Steam user,
However, the game is still not without it's flaws. There's always room to improve and one such area is the way ETA is calculated to a planet. If you've ever charted a path to a monument and engaged pulse, you'd know that the ETA is more of an extremely aggressive guess to reach the landmark versus the time it actually takes. Note that it's accurate for when you're about to drop out of warp or hit a planet's atmosphere, so I'm only specifically targeting landmarks on the planet's surface.
And hence, I'm going to try to see if I can build a more accurate model for determining the time it takes to reach that planet's landmark.
Logging the distance from the planet's landmark
It would help if we had had a precise way of measuring the distance to a landmark relative to time. Instead of doing this by hand, we can just sample the value from NMS.exe's process memory while it's running at fixed intervals and record it to a log file. We'll use the following to open the process in memory:
HANDLE pHandle = NULL;
HANDLE snapshot = CreateToolhelp32Snapshot(TH32CS_SNAPPROCESS, NULL);
if (Process32First(snapshot, &processEntry) == 1)
{
while (Process32Next(snapshot, &processEntry) == 1)
{
_bstr_t asChar(processEntry.szExeFile);
if (_stricmp(asChar, "NMS.exe") == 0)
{
pHandle = OpenProcess(PROCESS_ALL_ACCESS | PROCESS_QUERY_INFORMATION, FALSE, processEntry.th32ProcessID);
break;
}
}
}
And this code to log the data at given points in time:
const __int64 distAddr = 0x1D444BE4FCC;
std::chrono::steady_clock::time_point startTime = std::chrono::steady_clock::now();
while (cEntries < maxEntries) {
// Grab distance
float cDist = 0;
SIZE_T bytesRead;
BOOL result = ReadProcessMemory(pHandle, (void*)distAddr, &cDist, sizeof(cDist), &bytesRead);
if (!result) {
std::cerr << "Failed to access memory! Bytes Read: " << bytesRead << "/" << sizeof(cDist) << std::endl;
return -1;
}
// Log result
std::chrono::steady_clock::time_point cTime = std::chrono::steady_clock::now();
float countTime = static_cast<float>(std::chrono::duration_cast<std::chrono::milliseconds>(cTime - startTime).count()) / 1000.f;
logFile << countTime << "," << cDist << std::endl;
Sleep(80);
}
Note I slightly paraphrased the code for clarity. The full runnable code is available here: https://github.com/drakeor/NMS-Distance-Logger. Also note that this code is super rough and would need to be tweaked or improved upon to work with your setup as the address is definitely going to be different.
How off is the current ETA?
To improve the system, we experimentally need to determine what the ETA is versus the time it actually takes to reach the planet. I ran 8 trials with the following conditions:
- Time starts the second the pulse drives engage. Estimated ETA is recorded visually in the game.
- Time ends once I'm within 200u of the surface (This is approximately the time the ship will start to level out and you'll be able to land).
- I'm using the same planet and the same ship and always flying perpendicular to the landmark, so obviously this model will be different for different ships/planets/approach angles/etc.
Onto the results in nice graphical form:

Shifting the function up by a constant to line up with the other function will give us a more precise ETA, right?
I mean, technically yes, we could do that, but there's a lot of conditions attached to that statement. For example, although the distance between myself and the landmark are changing, the distance between the top of the atmosphere and the landmark remain the same along with the time it takes to reach the landmark from the atmosphere. It's a side-effect of the way I ran my trials. Shifting the Estimated Time up by (mean(Actual ETA) - mean(Estimated ETA)) gives us the following graph and our new shifted estimation function now has 3% error.

But we're not gonna stop there as there's still plenty going on behind the scenes I'd like to examine and eventually help us build a slightly more robust generalized model.
Examining distance over time for all trials
Below is a scatter plot of all eight trials by distance over time. Note that the x-axis is changed to represent ETA.
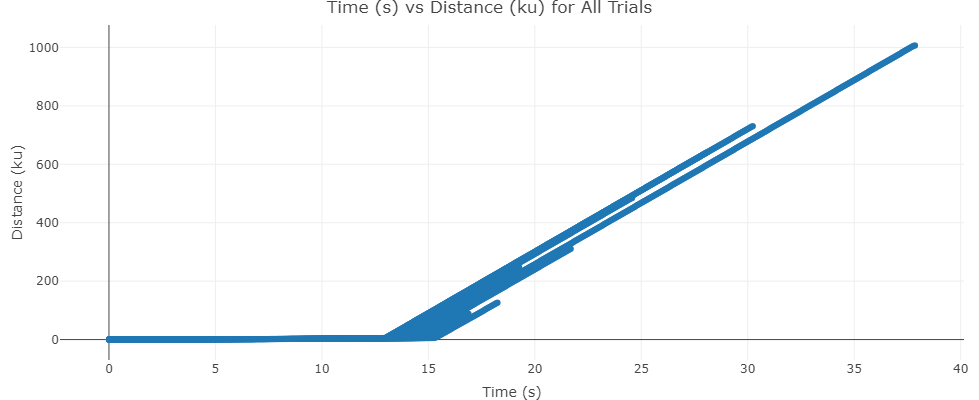
We can tell this represents a piecewise function with one piece representing traveling normally (piece A) while the other represents traveling with pulse engines (piece B):
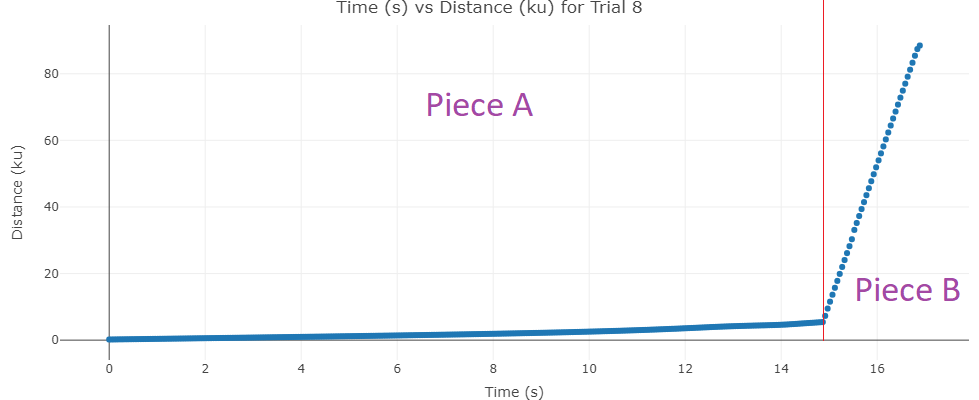
Piece B is obviously linear and we can find a line to it using least squares regression (R makes this pretty painless!). Piece A is deceiving as our velocity isn't constant. We are de-accelerating as we approach the surface, so the the change in velocity with respect to time is decreasing as well. We can fit to this using non-linear least squares regression. Mathematically, our function would look like this:
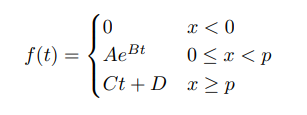
We just need to find constants A, B, C, and D. Using R makes this really easy. We're using lm to fit to a linear model for piece B, but for piece A, we need to take the logarithmic value and then determine the non-linear least squares estimates :
# Piece B
pieceB <- allTrialsdf[allTrialsdf$eta>boundaryP,]
pieceB <- pieceB[c("eta", "distInKU")]
lin_model <- lm(distInKU ~ eta, data=pieceB)
c <- lin_model$coefficients[[2]]
d <- lin_model$coefficients[[1]]
# Piece A
pieceA <- allTrialsdf[allTrialsdf$eta<boundaryP,]
pieceA <- pieceA[c("eta", "distInKU")]
exp_model <- lm(log(distInKU) ~ eta, data=pieceA)
a <- exp(coef(exp_model)[1])
b <- coef(exp_model)[2]
model <- nls(distInKU ~ a * exp(b * eta), data = pieceA, start = list(a = a, b = b))

So graphically, that discontinuity around p is pretty ugly. Our limit as t approaches p from the right is negative and therefore, at p, we expect to be buried 20ku in the ground. No Man's Sky still isn't the most stable game, so I wouldn't doubt if you could do that. To resolve this, we're going to take the max of the function of both piece A and B functions across a specific boundary. We can't do this across the whole domain since A is an exponential function if we keep running along t, the function will suddenly snap back to an exponential form. Our new math equation looks like this:

And graphically, it looks much better. No more spatial anomalies or rapid disassembly while attempting to reach your target!
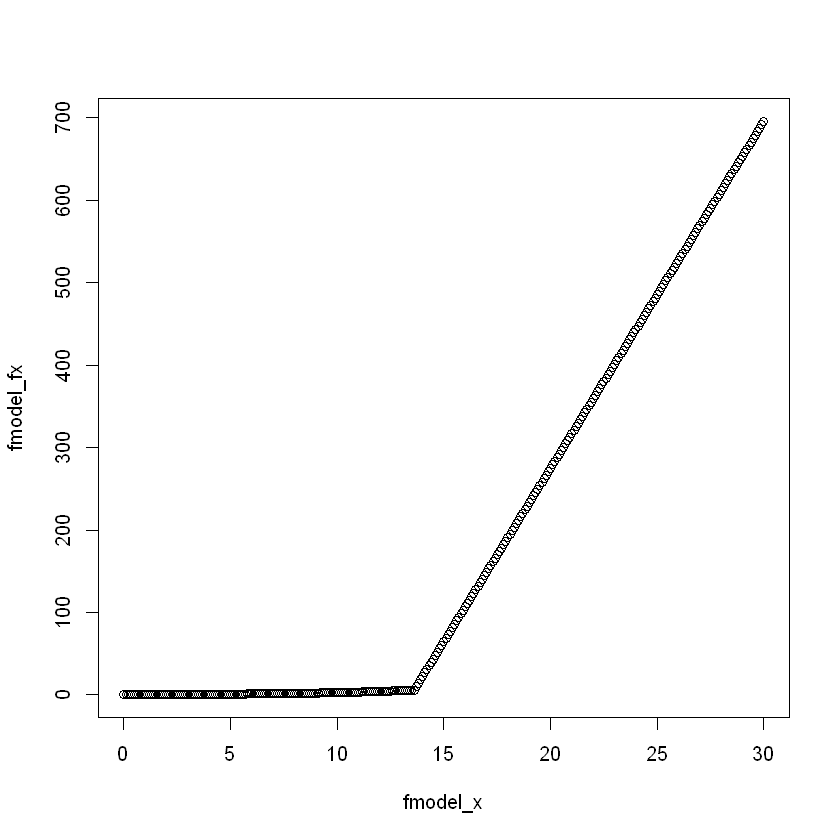
Finally, we'll see how well the model performed on the data I used to build it. (Somewhere a stats teacher and ML engineer felt a chill run down their spine and they can't figure why).
| Trial | Distance (ku) | Game Estimated Time (s) | Model Estimated Time (s) | Actual Time (s) | Model Error |
|---|---|---|---|---|---|
| 1 | 484 | 11 | 25 | 25 | 0% |
| 2 | 730 | 18 | 31 | 31 | 0% |
| 3 | 641 | 15 | 29 | 28 | 3% |
| 4 | 247 | 5 | 19 | 19 | 0% |
| 5 | 127 | 3 | 17 | 18 | 6% |
| 6 | 1007 | 23 | 37 | 38 | 3% |
| 7 | 311 | 7 | 20 | 22 | 10% |
| 8 | 88 | 2 | 15 | 17 | 13% |
That looks pretty good! Here's the final model with the axes flipped:
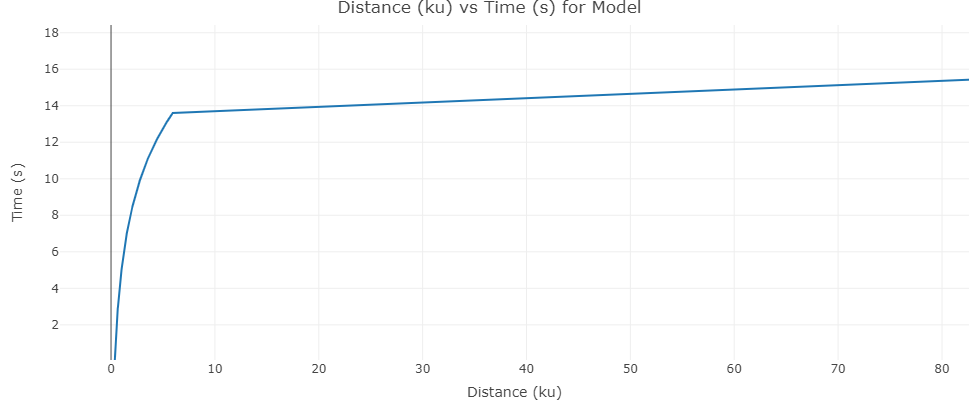
But still..
I could have gotten just as good of a result by shifting the function up and calling it a day. I could have probably gotten away with using a linear model for piece A. Pulse engines give us instant velocity, but what if we we're starting at zero velocity on a planet and going to a landmark? This whole model is extremely specific and applies only to my situation. It goes out the window as soon as one of the variables changes or we slap on a new module to our ship. The most I've proven is that if you're flying to a planet's landmark, the game's ETA system is inaccurate, but it's something we've all already known as we watch our ETA stay at 0:04 seconds for 0:08 seconds while approaching the surface.

Where do we go from here?
- The game's ETA system is accurate to when you hit the planet's atmosphere and leave warp. But that's pretty much a given
- I do not know if the height of the atmosphere is the same for all planets, and therefore do not know if a future model would need to be dependent on the height of the atmosphere. Hopefully it's just a constant value and not one I would need to mine.
- It would be interesting to see how approaching a landmark at a shallow/closer to parallel versus perpendicular in space.
- Ships vary in their max velocity as well as acceleration. Ships closer to the surface will fly slower than ships near the edge of space. We'd likely need to take this into account.
Conclusion
Obviously this model is only applicable to my set of conditions, but a more generalized model is definitely something I'd love to eventually build in the future. In the future when I have more time, I'd love to revisit this project.

