What is Block Sudoku?
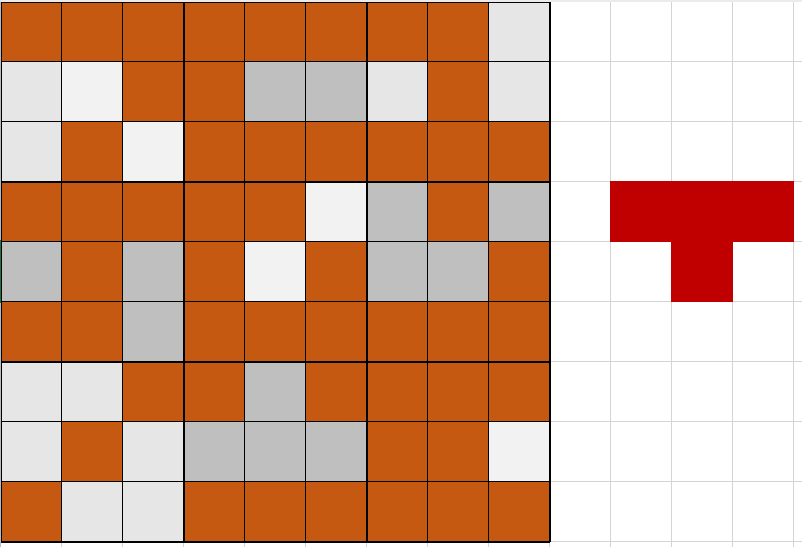
Block Sudoku is a game arranged like a traditional Sudoku board, and each "round", you place 3 tetris-like blocks on the board. They can be anywhere on the board as long as they don't collide with an existing piece on the board. An example is below:

But unlike Tetris, you cannot rotate the blocks. You gain points by clearing the blocks off the board. You can clear blocks either filling up a row, column, or one of the 3x3 squares. All of the following arrangements below are valid for clearing a line or block of blocks.

The game ends when you cannot place all three of the blocks you were given that round such as being left with the T-block on the board below and points are tallied:
Recreating Block Sudoku Logic
Of course before we can teach an AI to play the game, we should really rewrite the game ourselves! We also have the added bonus of releasing our own version of the game since the ones in the Android Play Store are riddled with ads. I opted to write this game in Python simply because I use Python for all my machine learning stuff already.
First up, the blocks. There are 22 different kinds of blocks and if we include rotations, this it adds up to 59 different configurations (I counted!). An L shaped block will look something like this in code while looking like this on the screen:
block_list.append( [[1,1,1,1,0],
[1,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0]])
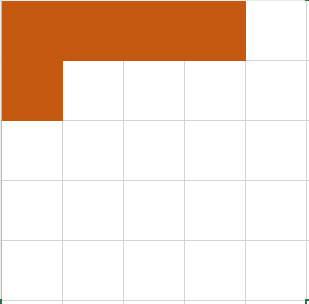
After the mundane task of coding all those blocks in, it was time to get to the board! The board is 9x9, but I opted to make mine 14x14 with the last five rows and columns full of ones as opposed to zeroes.
self.board = np.matrix([
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[0,0,0,0,0,0,0,0,0,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1],
[1,1,1,1,1,1,1,1,1,1,1,1,1]
])
This in turn allows us to write some pretty compact code for figuring out if we can place a block down on a certain square. We can simply add the block to the board and see if any of the values are over 1 (This indicates overlap). The extra padding of ones is so we can't insert a block (such as a 5x1 block) outside the bounds of the matrix and get all sorts of nasty python errors. The padding of 1s means that anything that goes out of bounds will automatically fail.
def check_if_valid_move(self, x, y, block):
# Make sure it's not outside our bounds
if(x < 0 or x >= 9):
return False
if(y < 0 or y >= 9):
return False
result_board = self.board.copy()
result_board[x:x+block.shape[0], y:y+block.shape[1]] += block
if(result_board.max() > 1):
return False
return True
We can naturally extend this function to check for a game-over state as well. If the following function returns 0 while a block is still in queue, then we have a game over state. We only need it to be greater than 1 for one of their blocks to allow the player to continue playing. (Okay optimally, we'd actually want to terminate the function immediately once we find a valid move rather than continue to iterate. I'm only continuing to iterate because I wanted stats on how many valid moves are possible!)
def get_all_valid_moves(self, block, board):
valid_moves = (9,9)
valid_moves = np.zeros(valid_moves)
for x in range(9):
for y in range(9):
valid_moves[x][y] = self.check_if_valid_move(x, y, block, board)
return valid_moves
Committing a move is just as compact and borrows from the check_if_valid_move function.
def place_block(self, x, y, block):
if not self.check_if_valid_move(x, y, block):
return False
self.board[x:x+block.shape[0], y:y+block.shape[1]] += block
We're actually almost already done with the core gameplay logic of the game! All that's left now is the code to clear the rows, columns, and 3x3 blocks whenever they get full. We also want to add to the player's score whenever they clear some blocks. In the Android versions, you get extra points for combos, so I just squared score to represent the extra points. I'm still on the fence whether or not I want to keep that in..
def clear_blocks_and_score(self, board):
# Score the rows first
score = 0
row_mask = np.floor(board[:9,:9].sum(axis=0)/9)
score += row_mask.sum()
row_array = np.repeat(row_mask, repeats=9, axis=0)
# Score the columns next
column_mask = np.floor(board[:9,:9].sum(axis=1)/9)
score += column_mask.sum()
column_array = np.repeat(column_mask, repeats=9, axis=1)
# Score the subblocks last
sub_matrix_mask = [[0,0,0],[0,0,0],[0,0,0]]
sub_matrix_array = np.matrix(np.zeros((9,9)))
for i in range(3):
for j in range(3):
sub_matrix_mask[i][j] = np.floor(board[(i*3):(i*3)+3,(j*3):(j*3)+3].sum() / 9)
if(sub_matrix_mask[i][j] == 1):
sub_matrix_array[(i*3):(i*3)+3,(j*3):(j*3)+3] = 1
sub_matrix_mask = np.matrix(sub_matrix_mask)
score += sub_matrix_mask.sum()
# Add the arrays together to figure out how to clear the board
combined_array = np.add(row_array, column_array)
combined_array = np.add(combined_array, sub_matrix_array)
combined_array = 1-np.clip(combined_array, 0, 1)
# Finally commit to the new board
board[:9, :9] = np.multiply(board[:9,:9], combined_array)
return score*score
Alright, before we can get real creative trying to solve this game, we need to establish a baseline. That is, I should probably play this game and see what sort of scores I'm able to achieve.
Console based Block Sudoku
We're so close to being able to play! After implementing a basic game loop and some game code, we now have a game fit for a lower-division intro to programming course!
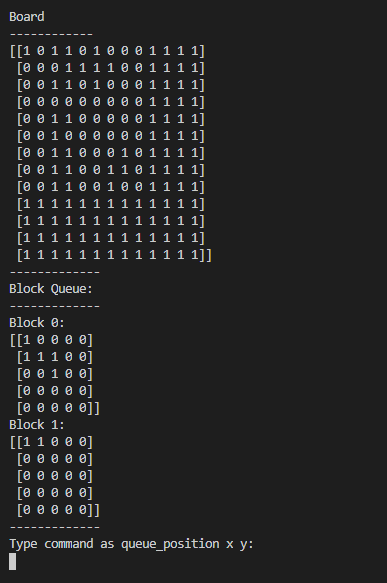
I created this simple console-based version to capture my baseline scores, but that quickly ended after 10 minutes of both equally boring and tedious gameplay. I felt that I might as well build it into something a bit more intuitive and impressive.
That'll come in Part 2..

