Introduction
This is a project I wrote last month for a parallel programming class as a way to test the performance of the ray tracing algorithm on both OpenMP and MPI. It's written primarily in C and requires no external libraries to run. The code in general is a bit of mess, but my main focus was comparing the OpenMP to the MPI implementations for my class.
What is Ray Tracing?
Put very briefly, the ray tracing algorithm works by virtually projecting a ray from a camera through each pixel on an image (which in our case is the screen) to represent the behavior of a light ray. It's very mathematically intensive operation, especially with reflective and near-transparent surfaces taken into account. Most modern implementations are done on GPUs.
Implementing Ray Tracing
The very first thing I needed to do was set up a virtual camera which was done by establishing a virtual eye that shoots rays through each pixel in an image. This is the image that will eventually be saved as a bitmap and displayed to the user. Just like real life, I'll only see light if it's reflected into the virtual camera. We can represent a ray and pixel pretty easily as:
/* I had issues with gcc padding so declaring this as packed helped and made it work with the image rendering functions */
struct Pixel {
unsigned char blue;
unsigned char green;
unsigned char red;
} __attribute__((__packed__));
/* Easy struct to represent a ray */
struct Ray {
vec3 origin;
vec3 direction;
int validRay;
};
And we can cast rays out of the eye and through the image with the following code:
void TraceRay(float* eyePos, float* screenPixel, float* outRayColor)
{
/* enable debug if we are on the debug pixel */
DEBUG_RAY_IMAGE = 0;
if(screenPixel[0] == DEBUG_COORDINATE_X && screenPixel[1] == DEBUG_COORDINATE_Y)
DEBUG_RAY_IMAGE = 1;
/* calculate the direction of vector */
vec3 direction;
vec3_sub(direction, screenPixel, eyePos);
vec3 norm_direction;
vec3_norm(norm_direction, direction);
/*
* Convert it to a Ray.
* It's important that direction is normalized (as described in the PBR book) as
* it's one of the common pitfalls
*/
struct Ray currentRay = InitRay();
vec3_dup(currentRay.origin, eyePos);
vec3_dup(currentRay.direction, norm_direction);
}
The scene is pretty barren so far as we have nothing to draw. One of the simplest shapes we can add to the screen is a sphere, which is mathematically represented as
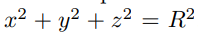
Shooting a ray through a sphere is essentially just solving for the intersection of a line and sphere which is easily solvable with the quadratic equation. One such example is listed at Paul Bourke's site. The translation of this to C looks like the following:
/*
* Calculate intersections for spheres
* Will return "2" if the ray completely misses
* - outNewRay and outCollisionNormalRay will be invalid
* Will return "1" if the ray is bounces.
* - outNewRay is the bounced array.
* - outCollisionNormal ray is populated
* - distance is populated
* Will return "0" if the ray is fully absorbed by the material.
* - outNewRay is will be invalid.
* - outCollisionNormal ray is populated
* - distance is populated
*/
int CalculateCircleCollision(struct Ray* originalRay, float* sphereCenter, float sphereRadius, struct Ray* outNewRay, struct Ray* outCollisionNormalRay, float* outDistance)
{
/*
* So we can represent a sphere like X^2 + Y^2 + Z^2 = R^2
* and the originalRay like U + Vx.
* Combining both and formatting it as a quadratic equation with x being x in Vx above,
* we can solve this using the quadratic formula and the disciminant will tell us
* if we have a solution
*/
vec3 deltaVec;
vec3_sub(deltaVec, (*originalRay).origin, sphereCenter);
/* Quadratic formula solving variables */
float a = vec3_mul_inner((*originalRay).direction, (*originalRay).direction);
float b = 2.0f * vec3_mul_inner((*originalRay).direction, deltaVec);
float c = vec3_mul_inner(deltaVec, deltaVec) - (sphereRadius * sphereRadius);
float discrim = b*b - 4.0f*a*c;
/* Default behaviour is invalid rays */
(*outNewRay).validRay = 0;
(*outCollisionNormalRay).validRay = 0;
if(DEBUG_RAY_IMAGE)
printf("discrim: %.2f\n", discrim);
/* If discriminant < 0, no solution. Ray misses. */
if(discrim < 0) {
return 2;
}
/* Otherwise solve quadratic for both roots */
float sol_a = (-b - sqrt(discrim)) / (2.0f * a);
float sol_b = (-b + sqrt(discrim)) / (2.0f * a);
/* Take the smaller of the too (if needed) */
float final_sol = sol_a;
if(sol_b < sol_a)
final_sol = sol_b;
if(DEBUG_RAY_IMAGE)
printf("quadratic solution 1: %.2f | solution 2: %.2f | final: %.2f\n",
sol_a, sol_b, final_sol);
/* This shouldn't happen. This means the sphere is behind the ray */
if(final_sol < 0) {
if(DEBUG_RAY_IMAGE)
printf("ray is behind camera! (ray misses)\n");
return 2;
}
/*
* Calculate the point of intersection.
* Since we calculated x (_final_sol) for U + Yx,
* we can get the exact point of intersection!
*/
vec3 hitIntersection;
vec3_scale(hitIntersection, (*originalRay).direction, final_sol);
vec3_add(hitIntersection, hitIntersection, (*originalRay).origin);
if(DEBUG_RAY_IMAGE) {
printf("collisionPoint: ");
vec3_print(hitIntersection, 1);
}
return 1;
}
To make things simple (and ensure my math is working correctly), I set that if the ray collides with the sphere, the pixel in the image will turn blue.

The distortion is caused by the field of view so the sphere does not appear perfectly circular. To properly shade the sphere, we need to calculate the reflection and implement diffuse lighting. Diffuse lighting is typically implemented off the concept of Albedo, which is "the measure of diffuse reflection of radiation out of total radiation". A value of 0 represents a black body, while a value of 1 represents a body that reflects all radiation.
To get the reflection angle, we can project a vector from the center of the sphere to the intersection point of our light ray from the camera. This will represent the normal that we can simply reflect the ray across. Adding on from our CalculateCircleCollision function above, we get
/* calculate the normal from the intersection point */
vec3 hitNormal;
vec3_sub(hitNormal, hitIntersection, sphereCenter);
vec3_norm(hitNormal, hitNormal);
if(DEBUG_RAY_IMAGE) {
printf("collision normal vector: ");
vec3_print(hitNormal, 1);
}
/* Update output collision normal ray */
vec3_dup((*outCollisionNormalRay).direction, hitNormal);
vec3_dup((*outCollisionNormalRay).origin, hitIntersection);
(*outCollisionNormalRay).validRay = 1;
*outDistance = final_sol;
/* flipped normal */
vec3 flippedNormal;
vec3_scale(flippedNormal, hitNormal, -1.0f);
/* Implement bouncing rays */
vec3 reflectedVector;
vec3_reflect(reflectedVector, (*originalRay).direction, flippedNormal);
vec3_norm(reflectedVector, reflectedVector);
vec3_dup((*outNewRay).origin, hitIntersection);
vec3_dup((*outNewRay).direction, reflectedVector);
(*outNewRay).validRay = 1;
After adding a simple point light in the scene, the results are much more convincing. Note that the point light also has fall off after a certain distance and obeys the inverse square law to calculate the light falloff.

After a bit of trial and error, I added a few more light sources and spheres. For handling the light from different light sources, I simply added the light sources together. I also compute the global max lighting value and automatically scale the lighting down to a value between 0 and 255 for the bitmap file. I've also added in planes which are defined by their normals. Calculating reflections and albedo is trivial.
/*
* Calculate intersections for planes
* Will return "2" if the ray completely misses
* - outNewRay and outCollisionNormalRay will be invalid
* Will return "1" if the ray is bounces.
* - outNewRay is the bounced array.
* - outCollisionNormal ray is populated
* - distance is populated
* Will return "0" if the ray is fully absorbed by the material.
* - outNewRay is will be invalid.
* - outCollisionNormal ray is populated
* - distance is populated
*/
int CalculatePlaneCollision(struct Ray* originalRay, float* planeOrigin, float* planeNormal, struct Ray* outNewRay, struct Ray* outCollisionNormalRay, float* outDistance)
{
outNewRay->validRay = 0;
outCollisionNormalRay->validRay = 0;
float denominator = vec3_mul_inner(planeNormal, originalRay->direction);
if(DEBUG_RAY_IMAGE) {
printf("plane normal:");
vec3_print(planeNormal, 1);
printf("original ray denominator:");
vec3_print(originalRay->direction,1 );
printf("plane denominator: %.2f\n", denominator);
}
/* infinite or no solutions. regardless, ray misses */
if(denominator < 0.0001f)
return 2;
vec3 deltaPosition;
vec3_sub(deltaPosition, planeOrigin, originalRay->origin);
float numerator = vec3_mul_inner(deltaPosition, planeNormal);
/* solve x for U + Vx which also is the distance */
*outDistance = numerator / denominator;
vec3 collisionPoint;
vec3_scale(collisionPoint, originalRay->direction, *outDistance);
vec3_add(collisionPoint, collisionPoint, originalRay->origin);
/* collision normal ray is easy: just the plane ray */
/* flip the normal though */
vec3 flippedPlaneNormal;
vec3_scale(flippedPlaneNormal, planeNormal, -1.0f);
vec3_dup(outCollisionNormalRay->direction, flippedPlaneNormal);
vec3_dup(outCollisionNormalRay->origin, collisionPoint);
outCollisionNormalRay->validRay = 1;
/* Handle reflections */
vec3 reflectedVector;
vec3_reflect(reflectedVector, (*originalRay).direction, flippedPlaneNormal);
vec3_norm(reflectedVector, reflectedVector);
vec3_dup((*outNewRay).origin, collisionPoint);
vec3_dup((*outNewRay).direction, reflectedVector);
(*outNewRay).validRay = 1;
return 1;
}
The final result of this looks like the follow:

In real life, light bounces everywhere and even surfaces not directly exposed to light are struck by indirect light. Since we already calculate surface normals, we can reuse those normals to reflect light rays and trace the path after each successive bounce. I also implemented an absorption/reflection factor that decreases the amount of light after each bounce. The reflectivity of the materials is also set pretty high (80 percent) to make this a bit more obvious. The end result is the following:

Performance
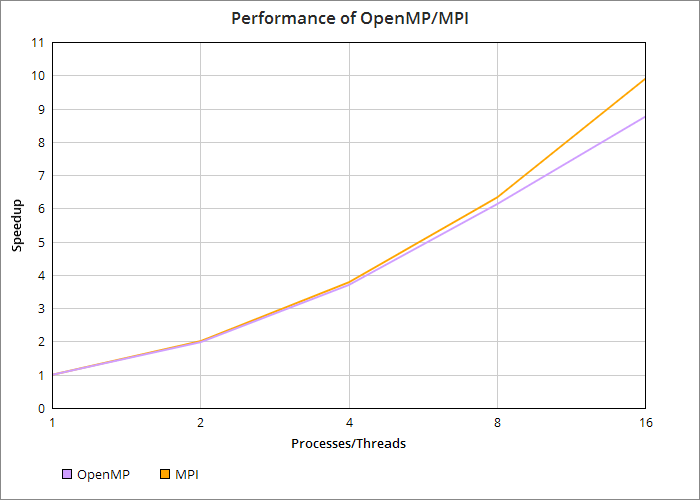
Below are the benchmarks for running a 1920x1072 scene in serial, OpenMP, and MPI. Note that I render the same exact scene each time for benchmark purposes.
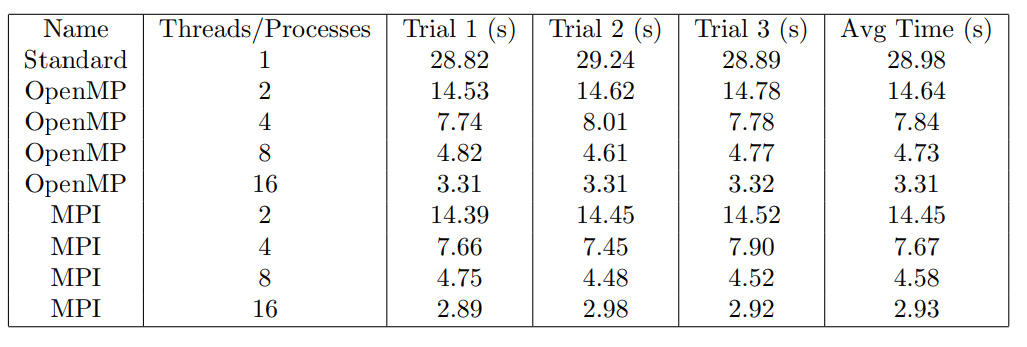
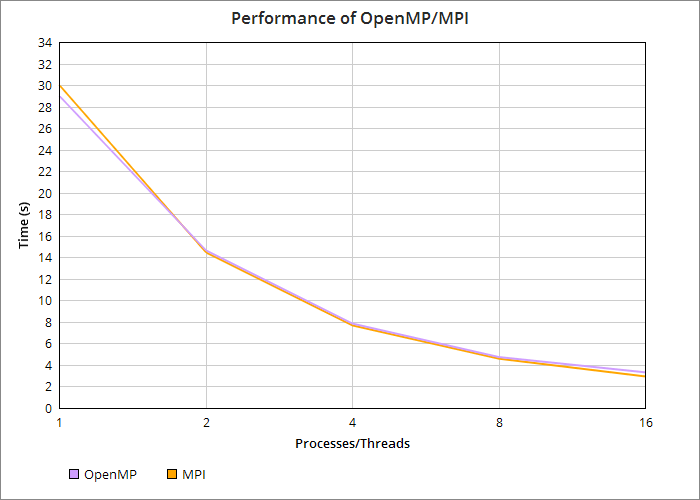
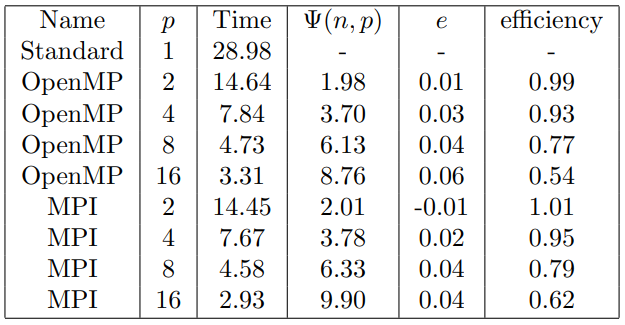
Below is the Karp-Flatt analysis along with efficiency for serial, OpenMP, and MPI. Interestingly, we get a superlinear speedup when moving from 1 to 2 processors in MPI.
Conclusion
Building a simple raytracer in C is pretty fun, but if I was to redo this project, I would definitely have built it in something like CUDA instead to take advantage of the GPUs.

